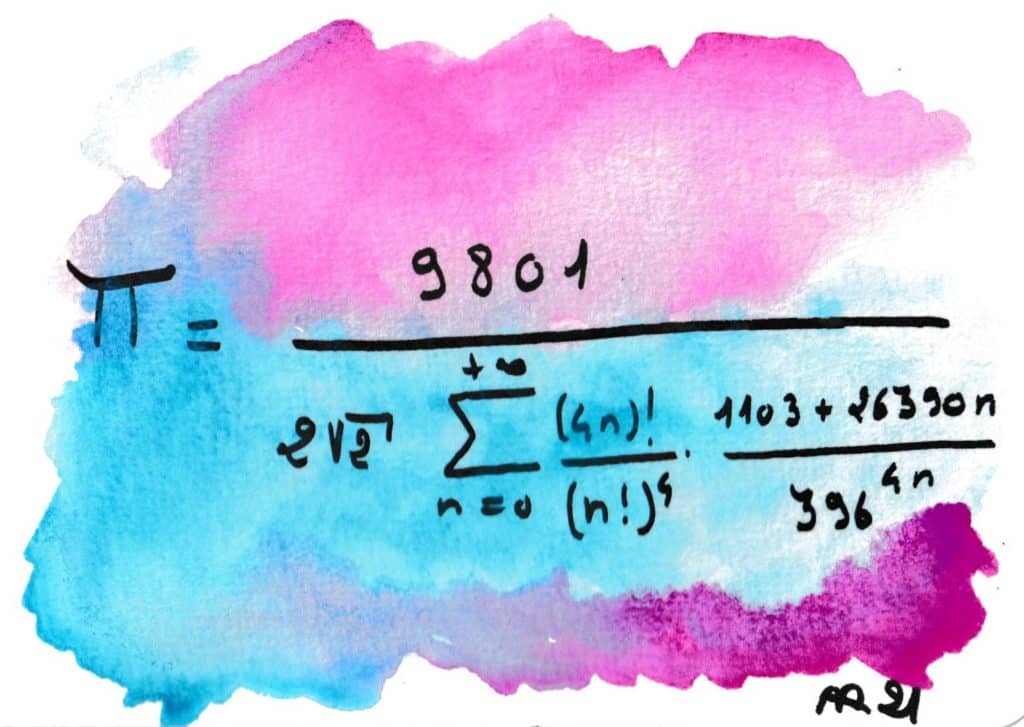Dessins d’Agnès Rigny, textes d’Emmanuel Amiot
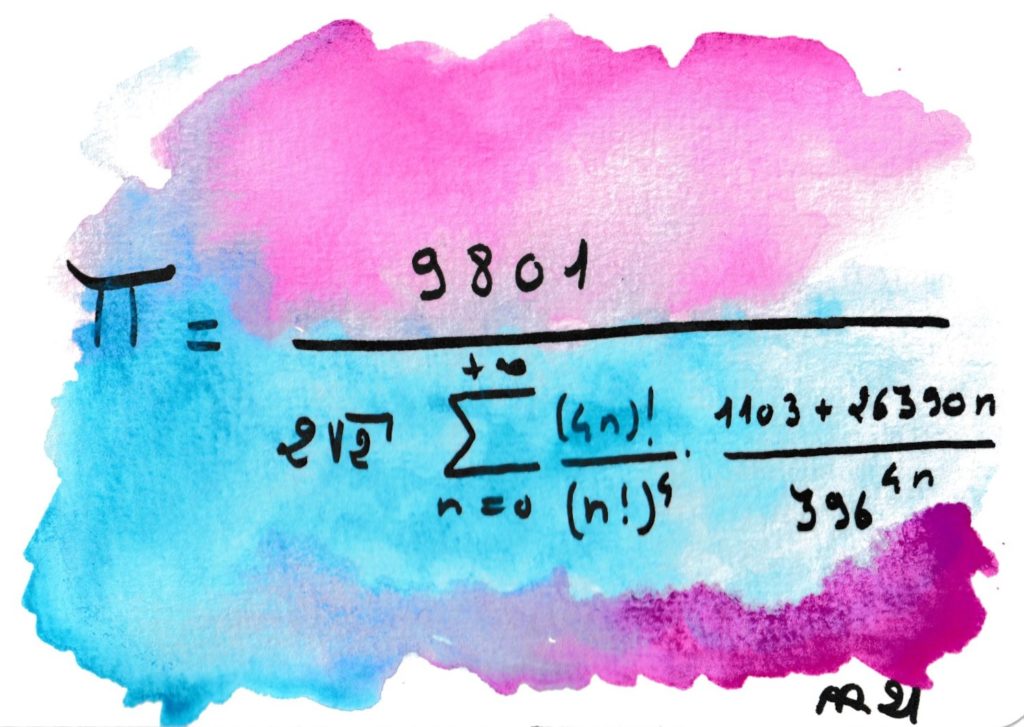
Srinivasa RAMANUJAN (1887-1920) est le Mozart des mathématiciens. Fascinant et mystérieux, il est mort jeune en laissant des milliers de formules non démontrées… et presque toutes vraies. Il laissait rarement des démonstrations, se disant inspiré par la déesse de son village natal, Namagiri Thayar. Cette formule n’est pas la plus efficace pour calculer π, mais elle laisse rêveurs même les plus endurcis des mathématiciens. Il a fallu plus de 70 ans pour qu’elle soit confirmée…
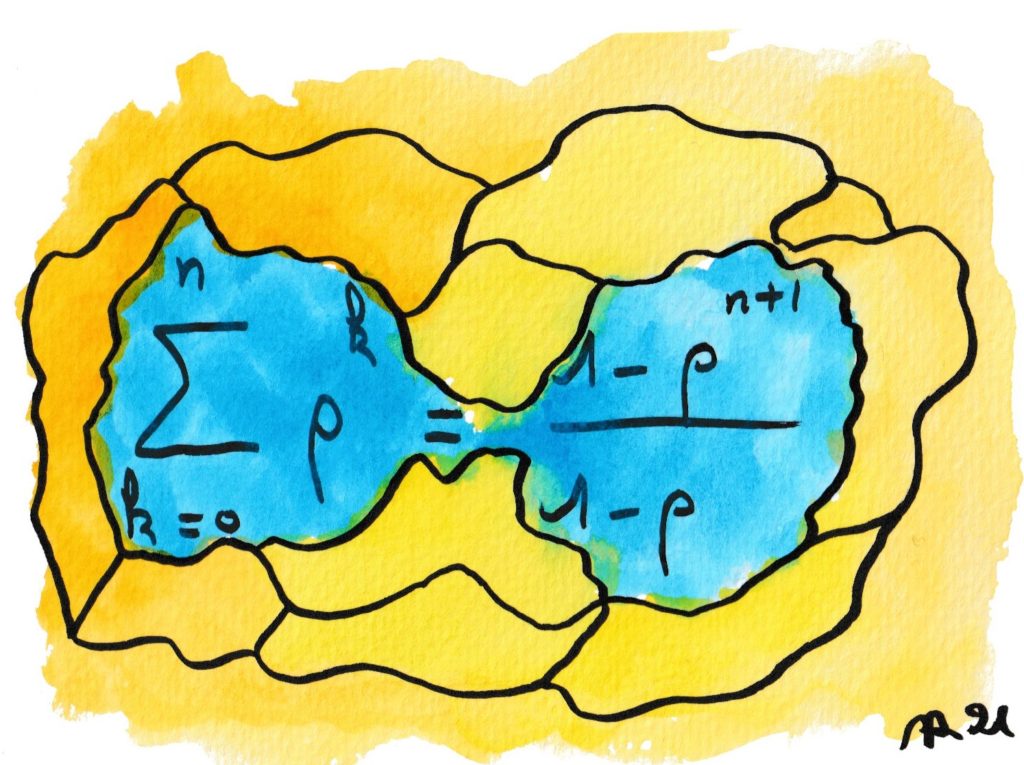
Cette formule est la base du calcul des séries. C’est un des rares cas où l’on est capable de savoir, à tout rang n, ce que vaut exactement la somme des n premiers termes — sans faire l’addition mais avec un calcul simple, celui du second membre. D’un côté, par exemple quand ρ=2 on perçoit le mystère de la croissance exponentielle (l’histoire des grains de riz sur l’échiquier). De l’autre, si ρ est assez petit cette expression a une limite, ce qui permet de résoudre le fameux paradoxe de Zénon d’Elée (Achille et la tortue).
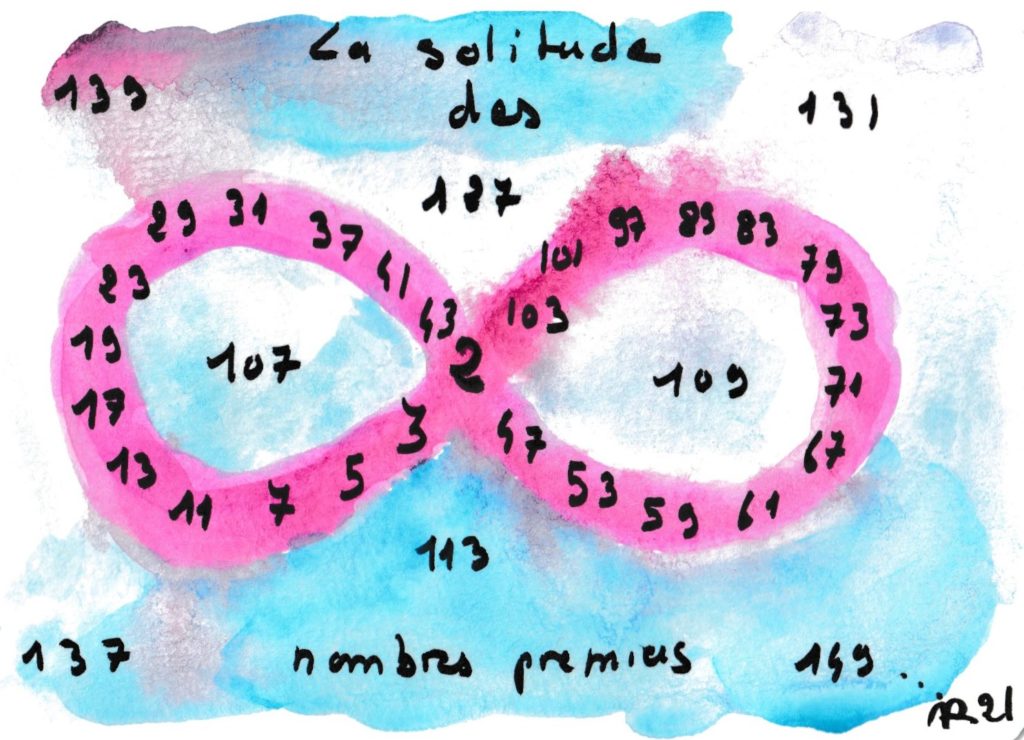
Euclide a démontré il y a plus de 2300 ans dans ses Éléments qu’il y a une infinité de nombres premiers, et sa démonstration reste la plus élégante. Mais on a toujours du mal à comprendre, aujourd’hui encore, l’irrégularité de leur distribution : parfois deux nombres impairs consécutifs sont premiers (comme 11 et 13), parfois l’écart est bien plus grand (entre n!+2 et n!+n, il n’y a pas de nombres premiers et donc l’écart est arbitrairement grand). En vérité, certains nombres premiers se sentent bien seuls.
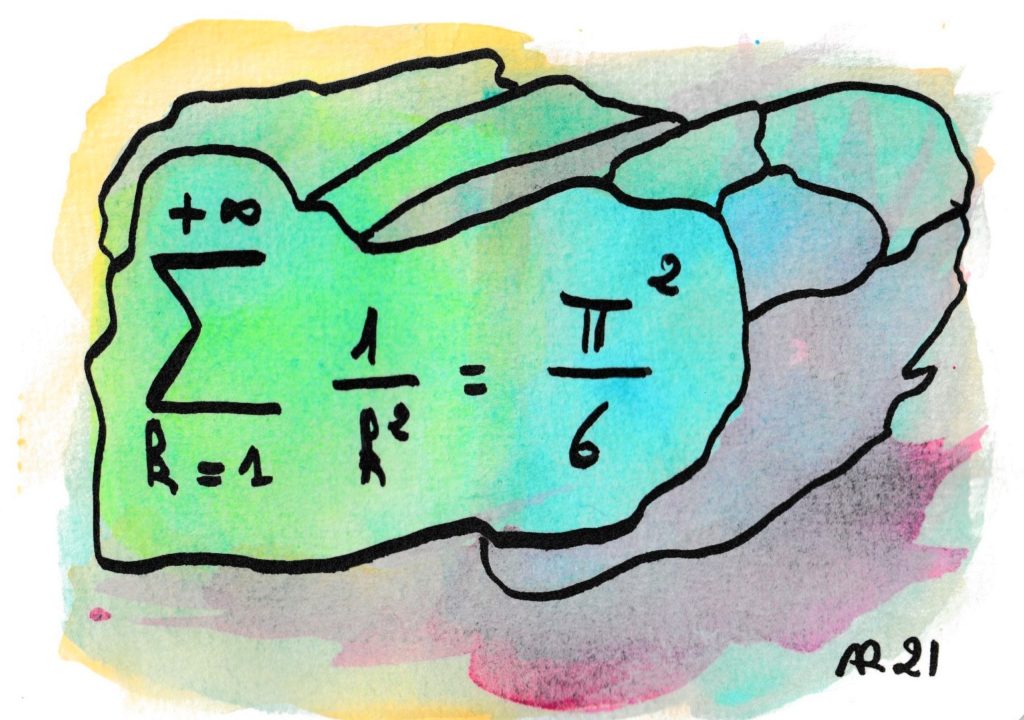
C’est le grand Léonard Euler qui a le premier trouvé la somme de cette série. La question remontait à un siècle (problème de Bâle) et Euler a deviné la valeur en 1735, grâce à sa maîtrise et sa précision dans les calculs numériques approchés et un calcul formel très audacieux. Ce résultat le rendit instantanément célèbre, par sa nouveauté et son côté exotique et insolite : mais que fait ce π² avec les carrés des entiers ?
Sa première démonstration rigoureuse attendra 1741. On sait calculer des formules analogues pour tous les exposants pairs, mais la généralisation de cette série (la fonction Zêta) recèle encore bien des mystères (hypothèse de Riemann).
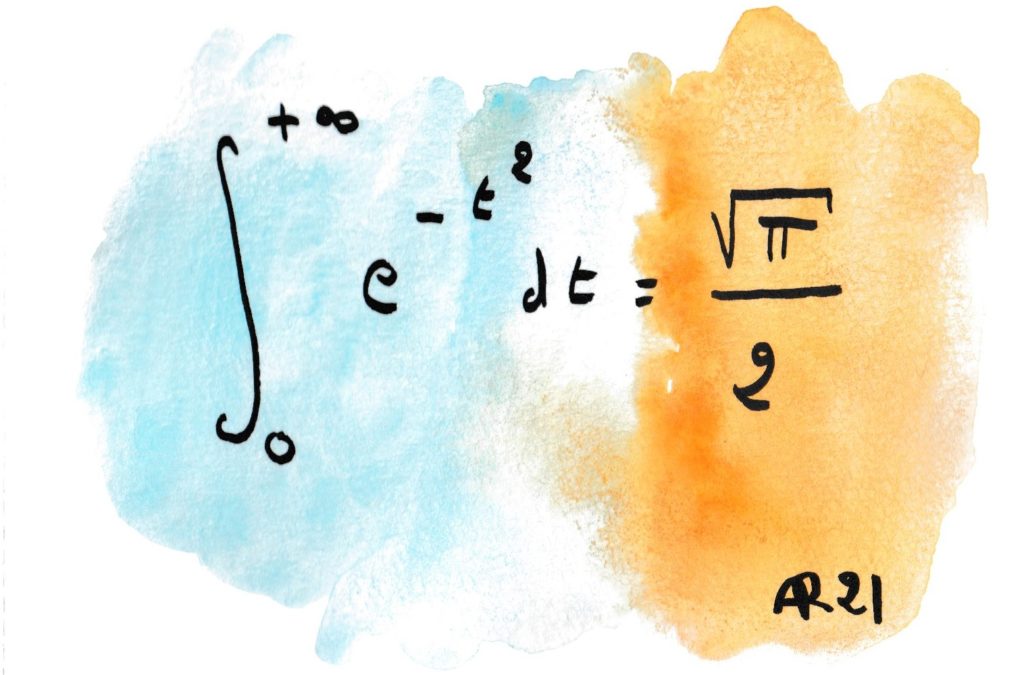
Cette formule stupéfiante est due à Karl Friedrich Gauss, le « prince des mathématiciens ». Même pour un spécialiste, la présence du √π reste mystérieuse (on peut l’expliquer, comme Gauss lui-même, en se ramenant des intégrales doubles sur des disques circulaires). Cette valeur est fondamentale pour la « loi normale » des probabilités, qui est le modèle vers lequel convergent les répétitions de phénomènes aléatoires quelconques, d’après la loi des grands nombres.
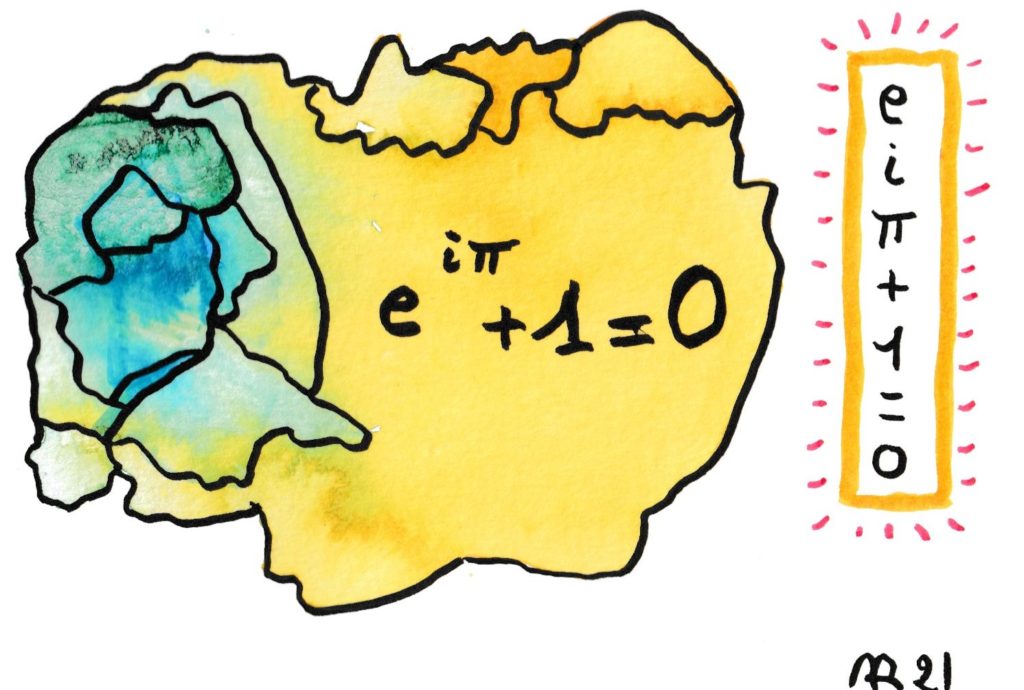
La plus belle formule des mathématiques selon Gauss ; elle relie les 4 constantes les plus fameuses : e, i, π et 1 !
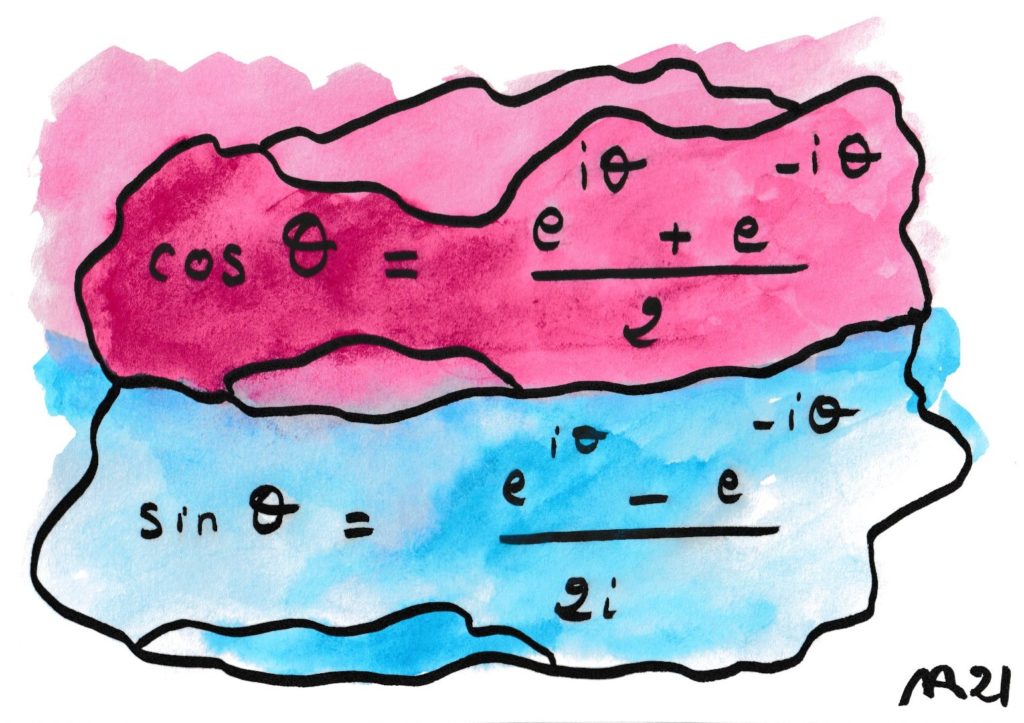
Ces formules extrêmement pratiques permettent d’obtenir TOUTES les formules de la trigonométrie à l’aide la propriété simplissime de l’exponentielle : exp(z+z’) = exp(z) exp(z’).
Euler a ainsi sans le savoir ouvert la porte de l’utilisation de la variable complexe dans les mathématiques modernes, un des sésames les plus fructueux depuis le XIXe siècle.
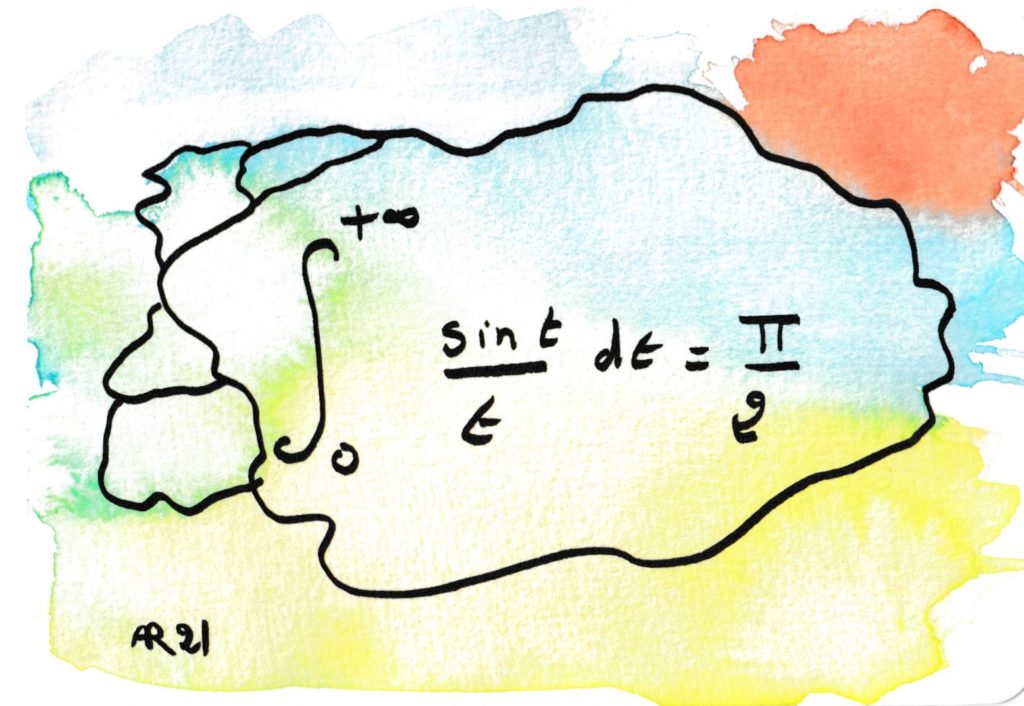
La fonction dans l’intégrale s’appelle sinus cardinal, elle a été introduite par Fresnel dans l’étude des vibrations lumineuses et leurs interférences. La valeur de l’intégrale est difficile à calculer. C’est un exemple célèbre d’intégrale semi-convergente.
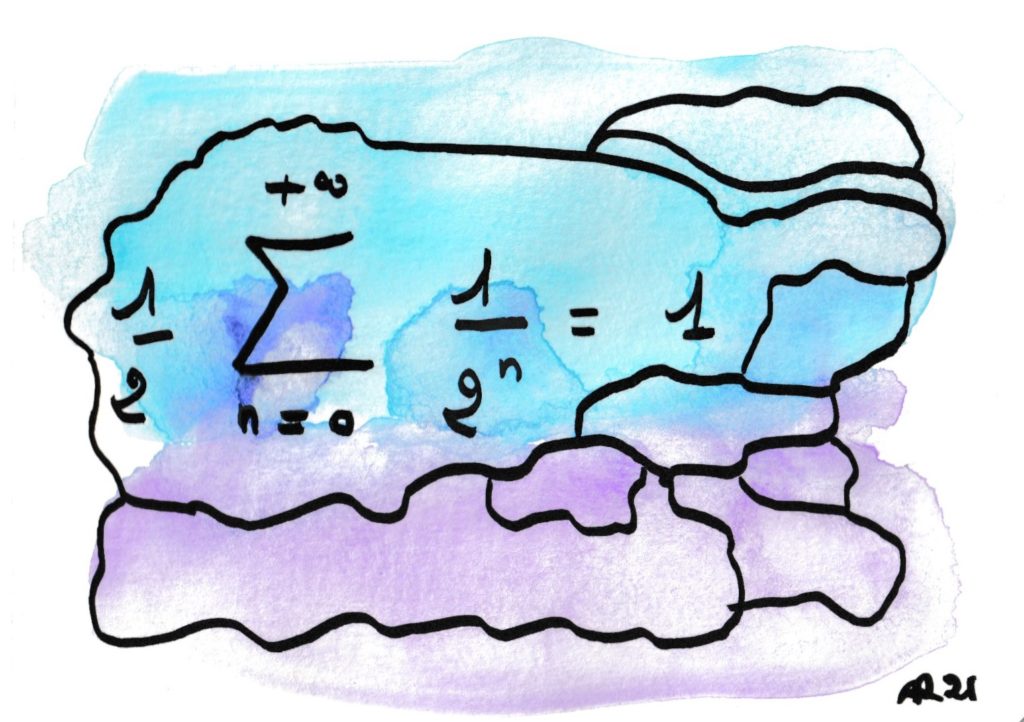
Cette formule est la première dans l’histoire de l’humanité qui envisage une somme d’une infinité de termes. Elle évoque le « paradoxe de Zénon », un sophiste d’il y a 25 siècles qui l’utilisait pour montrer l’impossibilité du mouvement : pour aller d’Athènes à Sparte, il faut d’abord faire la moitié du chemin, puis la moitié du reste, puis la moitié de cette moitié… et cela ne finit donc jamais ? !
En vérité il montrait plutôt la difficulté de modéliser le monde réel grâce aux idées — la définition rigoureuse des sommes infinies remonte au… XIXe siècle et suscite encore de féconds travaux de nos jours.
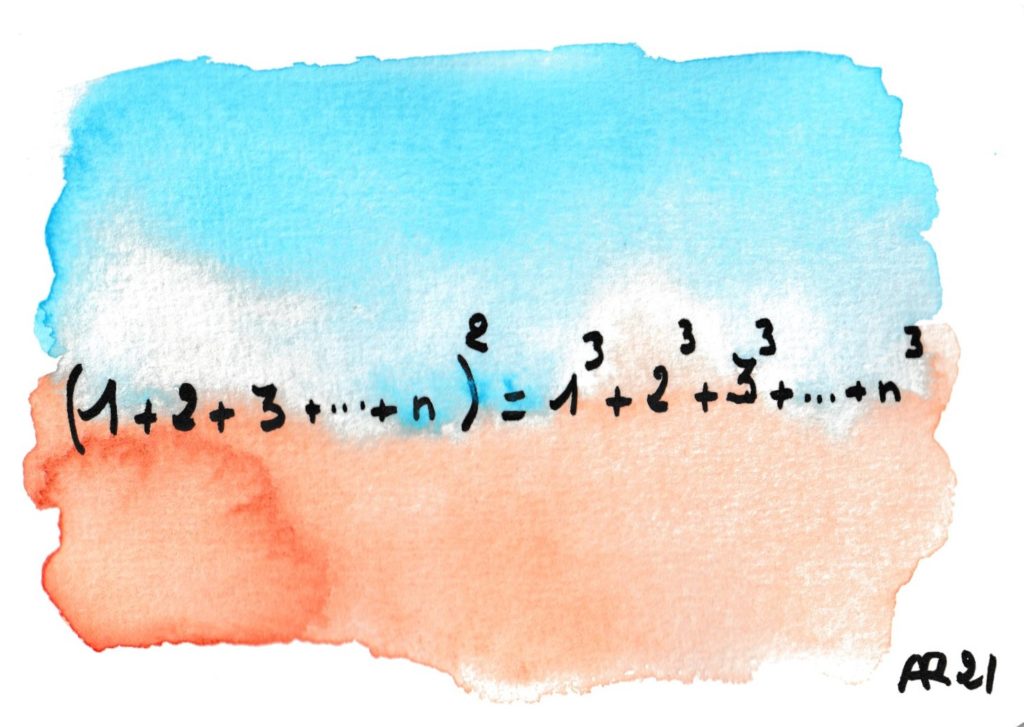
Il existe des formules pour les sommes des puissances kièmes, pour tout k (sommes de Newton). Il est miraculeux que la troisième (« somme des cubes ») soit le carré de la première…
Et pourtant il existe de ce fait des preuves géométriques !

Les écritures infinies ont toujours fasciné et continuent à interpeller, même si les mathématiciens modernes ont réussi à relativement bien maîtriser le monstre ! La question « (pourquoi) est-ce que 0,99999 est égal à 1 ? » est une des plus brûlantes sur Internet et remonte à l’antiquité grecque. Si on a le droit de poser x=0.99999… alors c’est facile, car un calcul élémentaire montre que 10x – x = 9 et donc x=1. Mais que cachent donc ces trois petits points ?
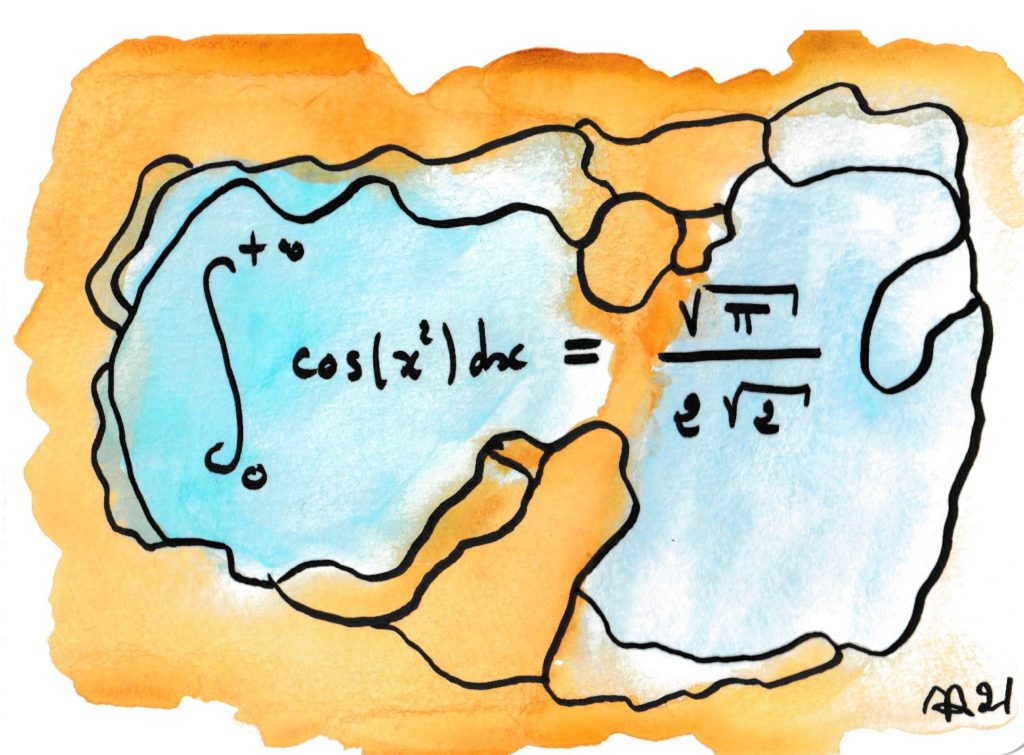
Déjà il n’est pas du tout évident que cette intégrale converge (intégration par parties avec de copieux préliminaires), et encore moins de calculer sa valeur. De plus, en la regroupant avec sa cousine en sinus on obtient une très belle courbe, la clothoïde ou spirale de Cornu, qui intervient aussi bien en optique que dans la construction de bretelles d’autoroute…

n! désigne le produit des entiers jusqu’à n. Cette suite tend très vite vers l’infini, mais son évaluation par rapport à des suites plus simples fait intervenir cet étrange facteur (racine de 2π). Cette belle formule (dite « de Stirling ») reste donc mystérieuse, même si elle est bien pratique.
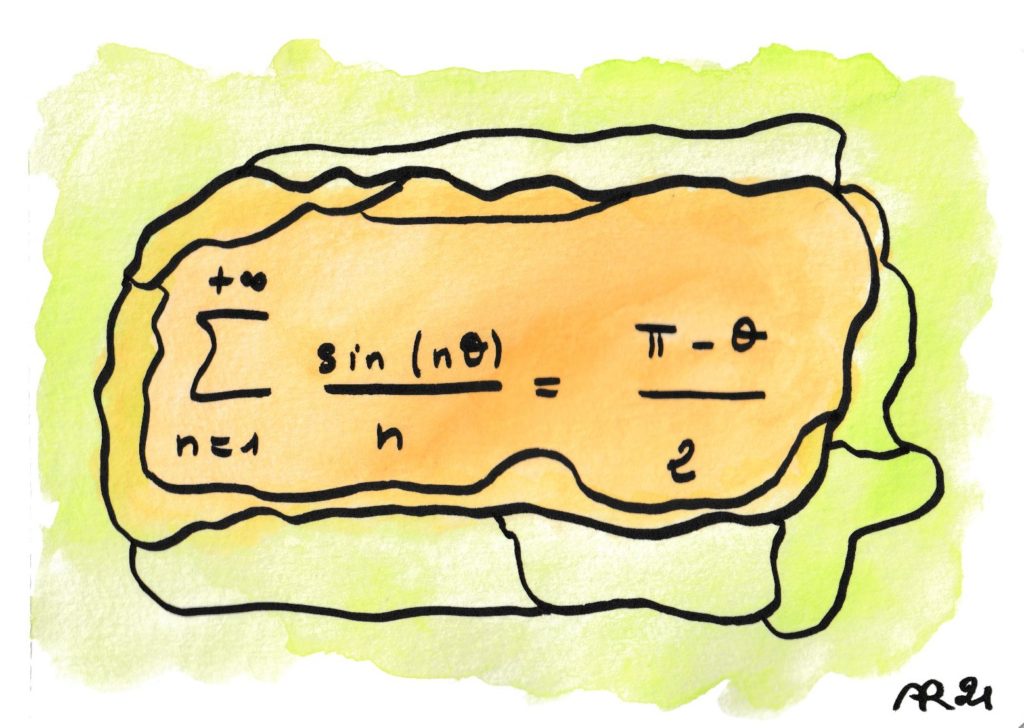
Cette formule peut surprendre car les sinus du membre de gauche sont des fonctions périodiques, oscillantes, alors que le membre de droite est l’équation d’une droite, rectiligne (l’égalité n’est en fait valide qu’entre 0 et 2π). De plus, alors que les sinus sont des fonctions on ne peut plus régulières, leur somme infinie devient discontinue. Ces mystères avaient échappé à Joseph Fourier, qui a eu néanmoins le mérite d’imaginer la possibilité de telles décompositions.
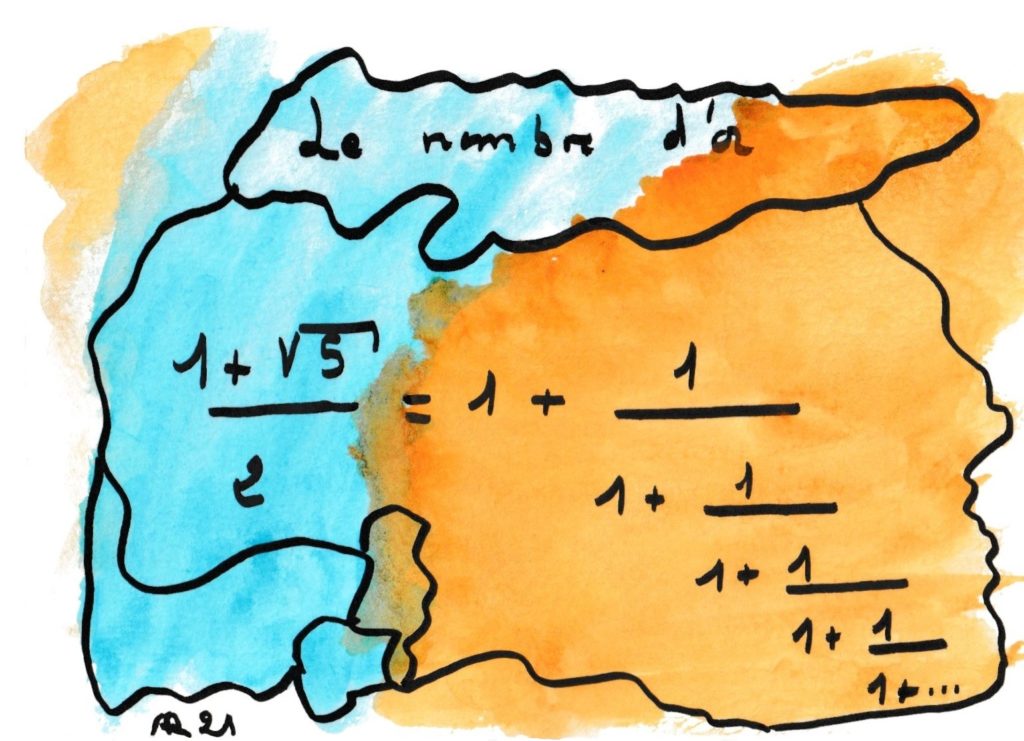
En fait, l’écriture du second membre comme un jaillissement de fractions imbriquées est possible pour tout nombre. Ce qui est remarquable pour le nombre d’Or est que tous les termes de la fraction soient égaux à 1. Selon certains, cette qualité qui fait du nombre d’Or l’irrationnel le plus mal approché par les rationnels ou le plus irrationnel de tous les irrationnels, explique sa prééminence en art et dans la nature, que ce soit dans le chou Romanesco ou la musique de B. Bartok.
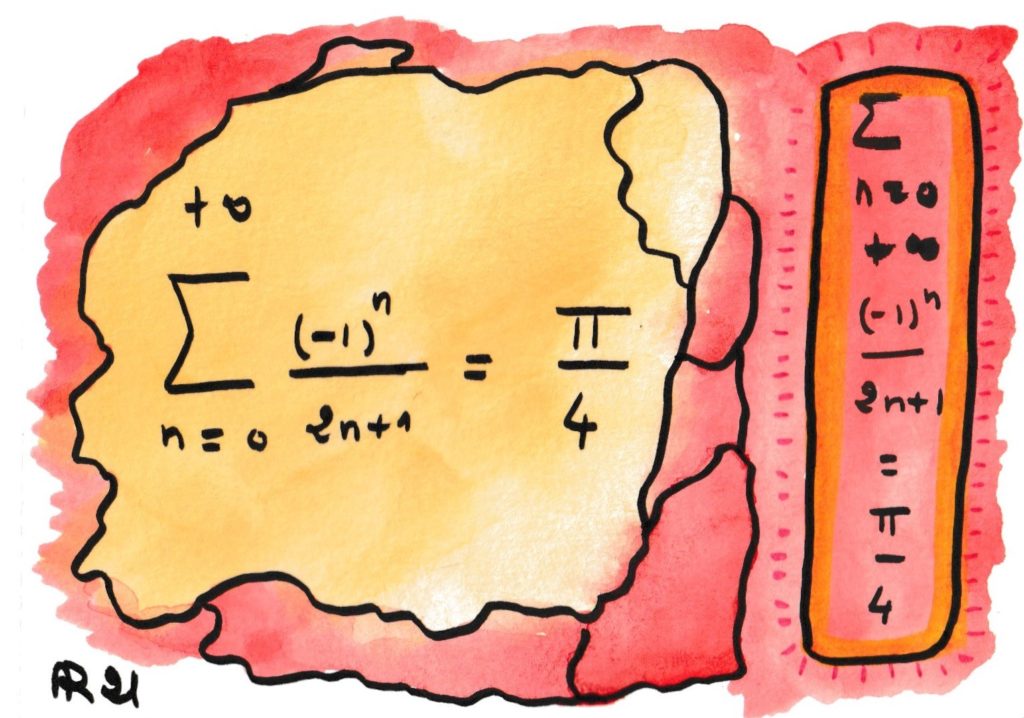
Déjà John Wallis avait exprimé le fameux nombre π (rapport de la circonférence d’un cercle à son diamètre) comme une limite de rationnels (fraction entre nombre entiers), mais sa formule était un produit assez compliqué. Au siècle suivant, G. Leibniz a découvert cette simplissime équation qui relie directement le nombre π à des sommes et différences d’inverses de nombres entiers.
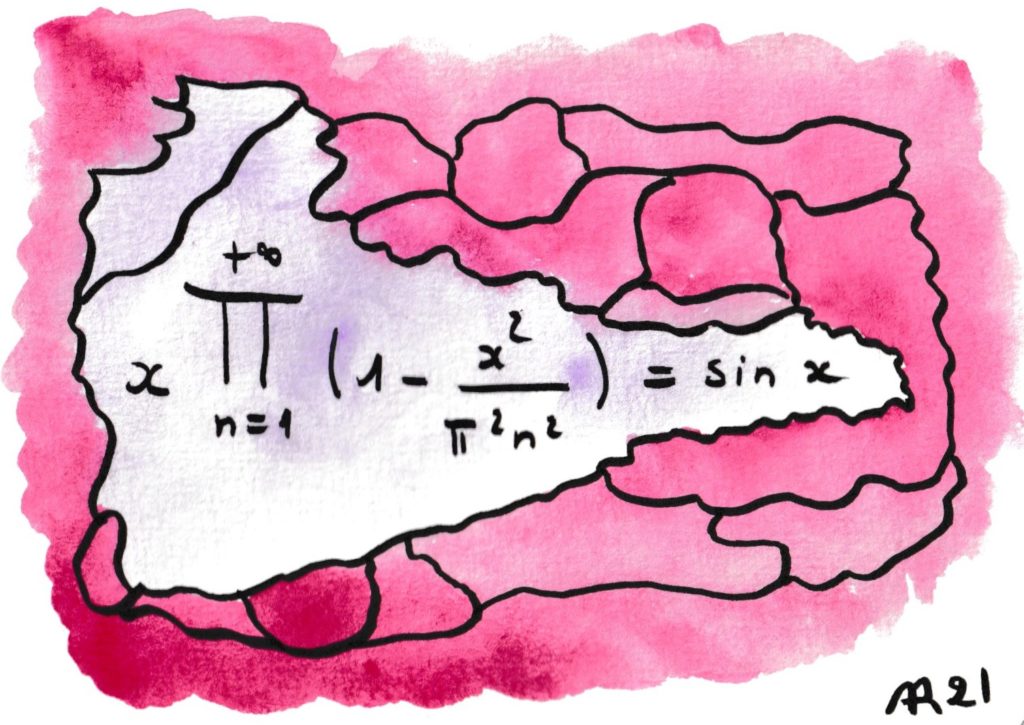
Dès le collège on peut réaliser que les deux membres coïncident quand x est un multiple entier de π : x = n π. En effet ils valent tous deux 0. Il est beaucoup moins évident que cela est vrai dans tous les cas (et même quand x est un nombre complexe), ce qui fut démontré par Euler, ce grand découvreur de formules stupéfiantes. Il utilisa celle-ci pour subodorer la solution du problème de Bâle.

Si la somme était infinie, le résultat serait 1 et vous le saviez sans doute déjà. Il n’est pas banal que la moitié de la somme s’obtienne en coupant au même rang n qui figure au dénominateur. Une des nombreuses interprétations possibles est la suivante :
Si vous revenez de la pêche avec en moyenne 10 poissons, alors le résultat médian de votre activité halieutique est aussi de 10 — il vous arrivera aussi souvent d’en ramener moins de 10 que 12, 13, 59 ou 147825 (!).
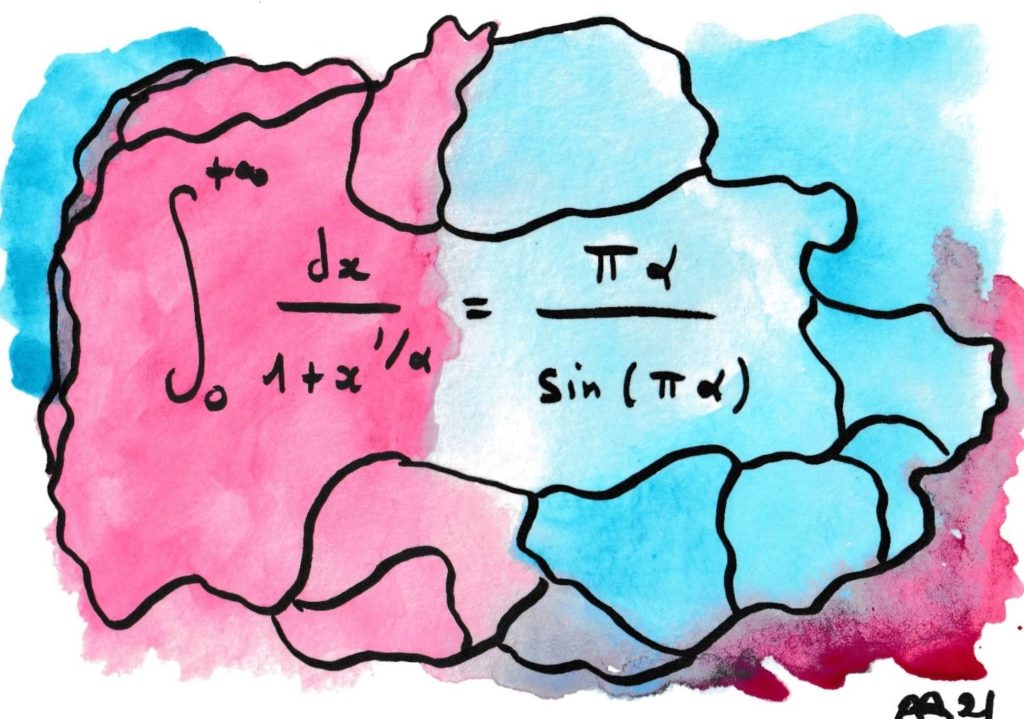
Ici le charme de la transcendance. Comment imaginer que l’expression sage de l’intégrale à gauche va faire apparaître l’inverse d’un sinus cardinal ?
D’autant que la démonstration la plus simple, si l’on ose dire, utilise un cheminement dans les nombres complexes, qui sont absents des deux membres !
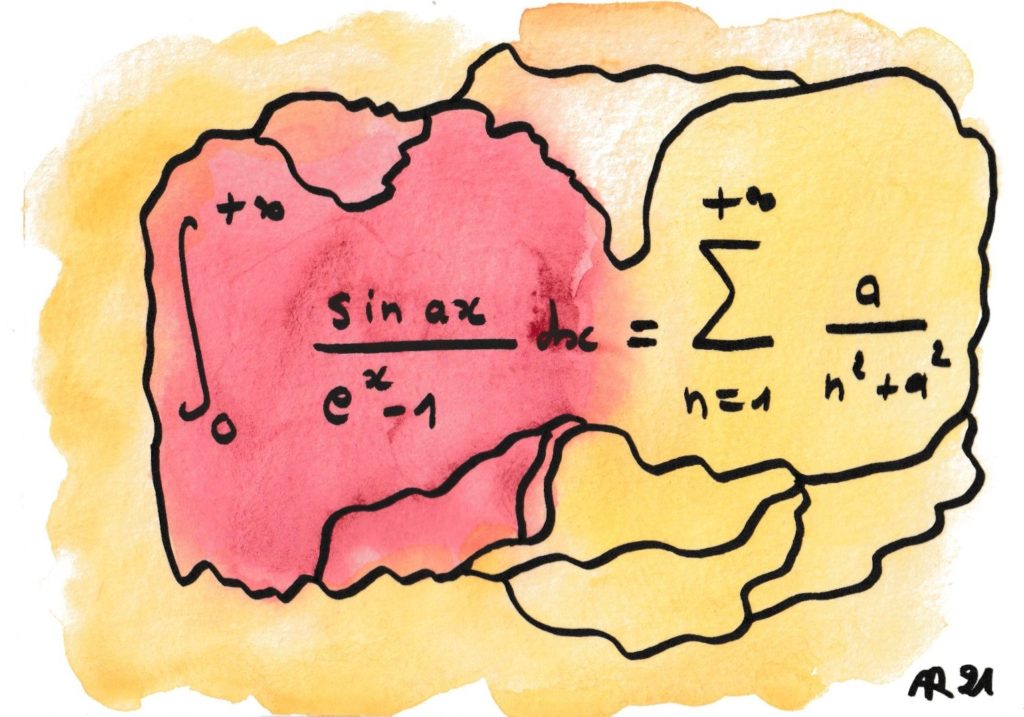
Deux grands mystères de l’analyse frémissent dans cette formule.
L’un est la transformation d’une somme infinie, mais discrète (∑ signifie « somme sur tous les nombres entiers ») en une somme continue, avec le symbole ∫ de l’intégrale, qui est une forme de somme sur tous les nombres réels entre 0 et l’infini.
L’autre est une des méthodes d’intégration terme à terme. Contrairement à l’intuition, il est rarement vrai que l’intégrale d’une somme (infinie) soit égale à la somme des intégrales, mais cette formule advient parce qu’ici, cela marche.
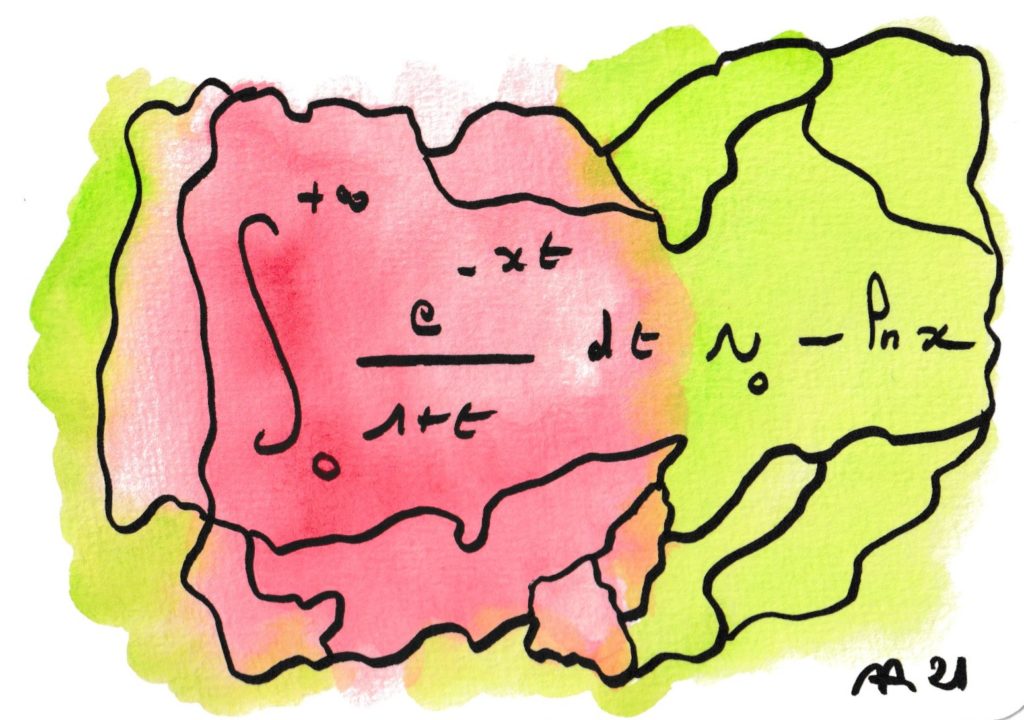
Quand x atteint 0, l’intégrale explose, c’est à dire tend vers l’infini. Mais à quelle vitesse cette explosion va-t-elle se produire ? Ce résultat indique que somme toute, cela ne va pas très vite, comme un log.
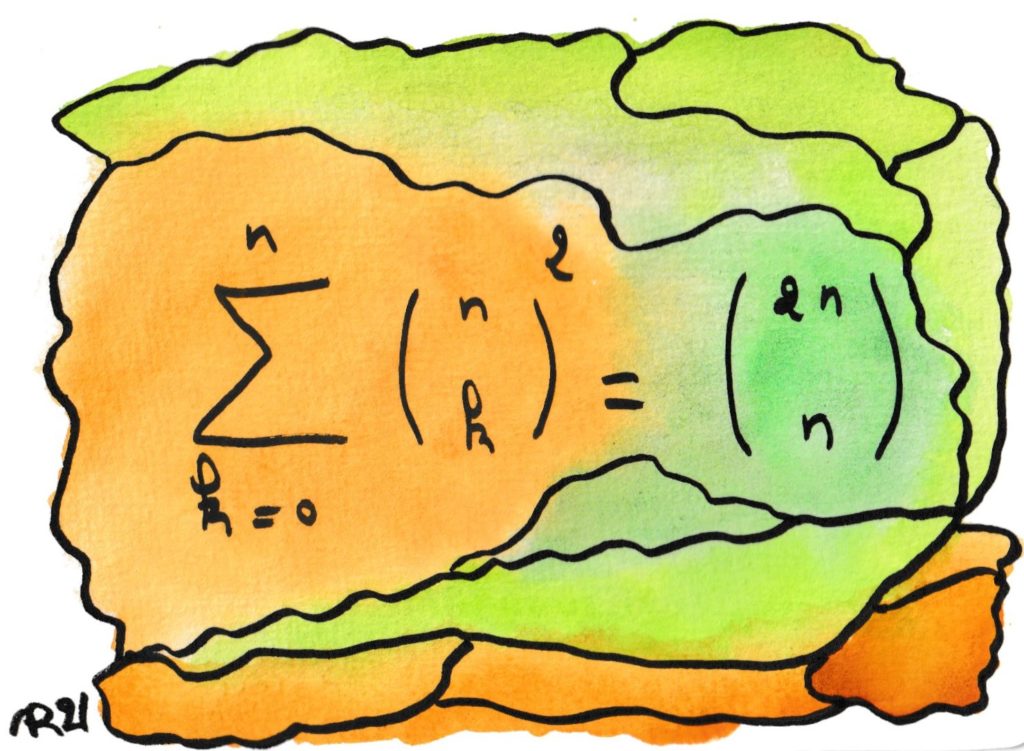
Cette formule pique-assiette se retrouve dans de nombreux domaines des mathématiques : fonctions, probabilités, dénombrements, polynômes…
Une interprétation, qui peut même servir de preuve, est que choisir 10 fruits parmi 10 pommes et 10 oranges, revient à prendre k pommes et 10 –k oranges avec k allant de 0 à 10, ce qu’un enfant affamé comprendra immédiatement 🙂
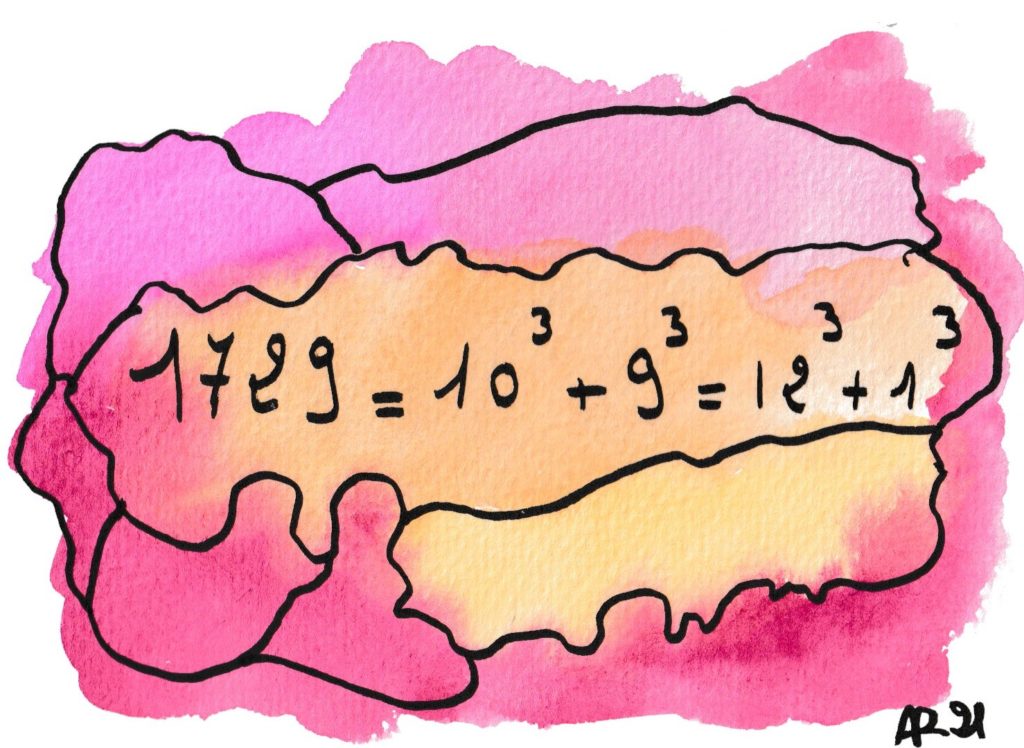
L’anecdote la plus célèbre de l’histoire des mathématiques ! En 1918, Hardy visitait son ami indien Ramanujan (qui se mourait de carences alimentaires) et pour parler de choses et d’autres, mentionnait que le numéro de son taxi, 1729, n’avait pas grand-chose d’intéressant. Ramanujan releva vivement la tête et rétorqua : « au contraire ! c’est le plus petit nombre entier qui s’écrive de deux façons distinctes comme somme de deux cubes d’entiers » !!!
Défi : trouverez-vous la solution du même problème avec les sommes de deux carrés ? C’est bien plus facile.

Beaucoup de visiteurs auront reconnu que 22/7 est une bonne valeur approchée du fameux nombre π. Elle était connue en Egypte antique et a été démontrée rigoureusement par Archimède. Cette formule exprime de manière exacte leur différence, l’erreur commise en remplaçant π par cette fraction simple ; et ce par une élégante intégrale, à l’expression concise et symétrique.
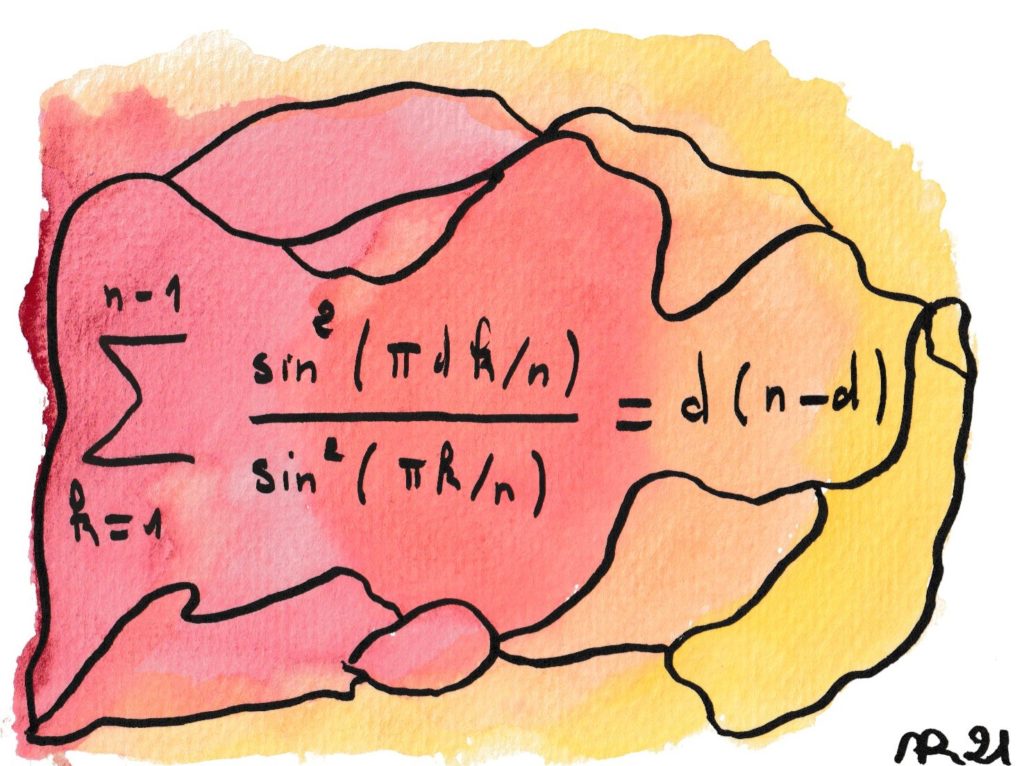
Les mathématiciens utilisent volontiers l’adjectif « élémentaire » pour qualifier un résultat qui n’utilise pas une théorie sophistiquée. À ne surtout pas confondre avec « facile » ! Cette formule découle facilement de considérations d’assez haut vol (conservation d’énergie lors d’une décomposition de Fourier discrète), mais on peut aussi la démontrer « élémentairement » — au prix de grands efforts.
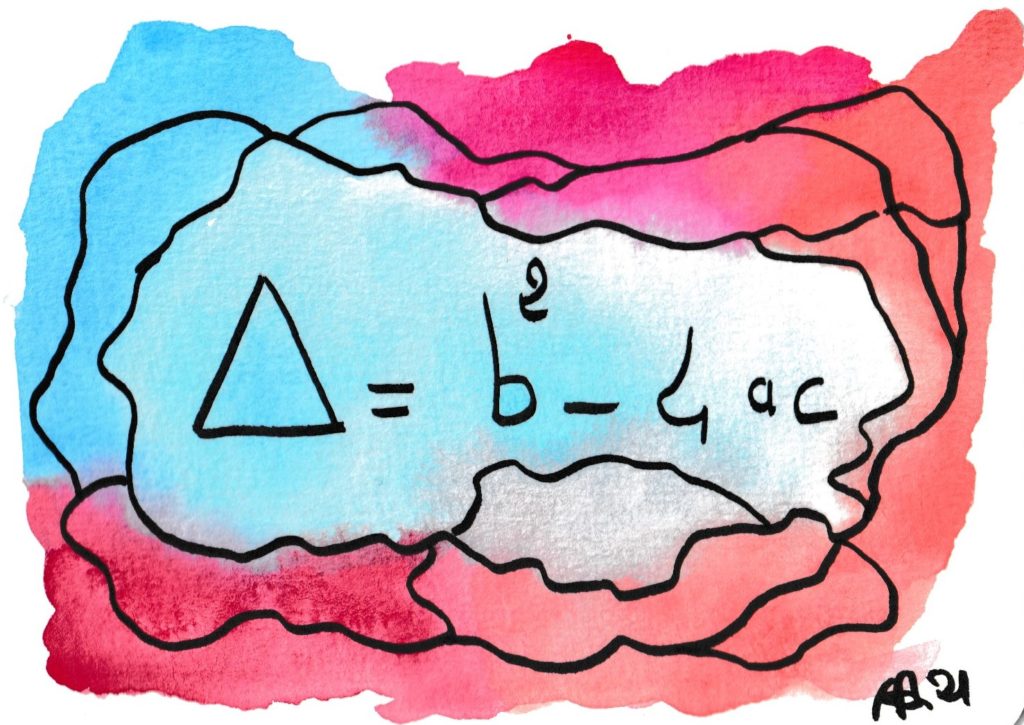
Qui ne se souvient de cette quantité fameuse ? Son signe détermine l’existence (en fait, la réalité) des racines d’une équation du second degré. Il aura fallu des siècles (entre Euclide et Al Khuwarizmi ) pour mettre le doigt dessus. Pour la plupart des adultes, elle aura cessé d’effrayer. Mais si je vous disait que c’est une forme quadratique, et qu’elle est égale au résultant d’un polynôme et de sa dérivée ?…
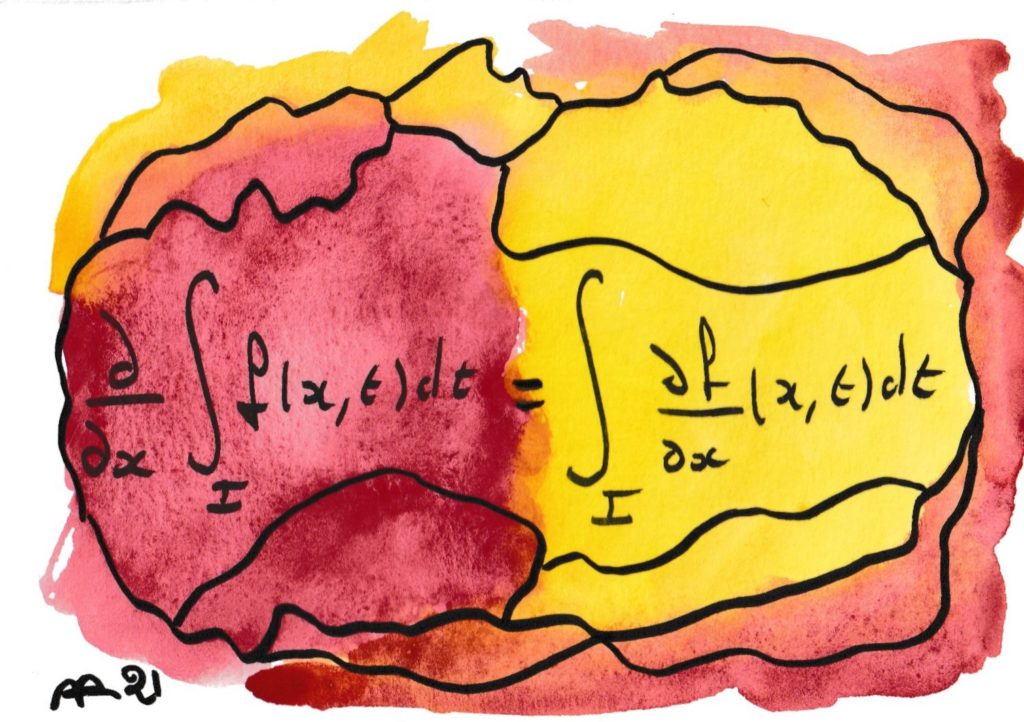
Cette formule interpelle par son apparente évidence : même sans connaître le sens des symboles, on « voit » qu’il s’agit simplement d’échanger la place deux d’entre eux. Eh bien parfois cela n’est pas un problème : 3×14 est bien égal à 14×3. Mais c’est souvent faux : 5/2 ≠ 2/5 ! Et de fait, la formule est fausse si l’on ne donne pas de conditions supplémentaires sur la fonction f (par exemple, elle doit être intégrable ainsi que sa dérivée partielle). Plus généralement, de nombreuses affirmations apparemment évidentes reposent sur une interversion de symboles qui ne va pas de soi, et une grande part de l’Analyse mathématique consiste à dresser des règles qui autorisent à le faire en toute légitimité.
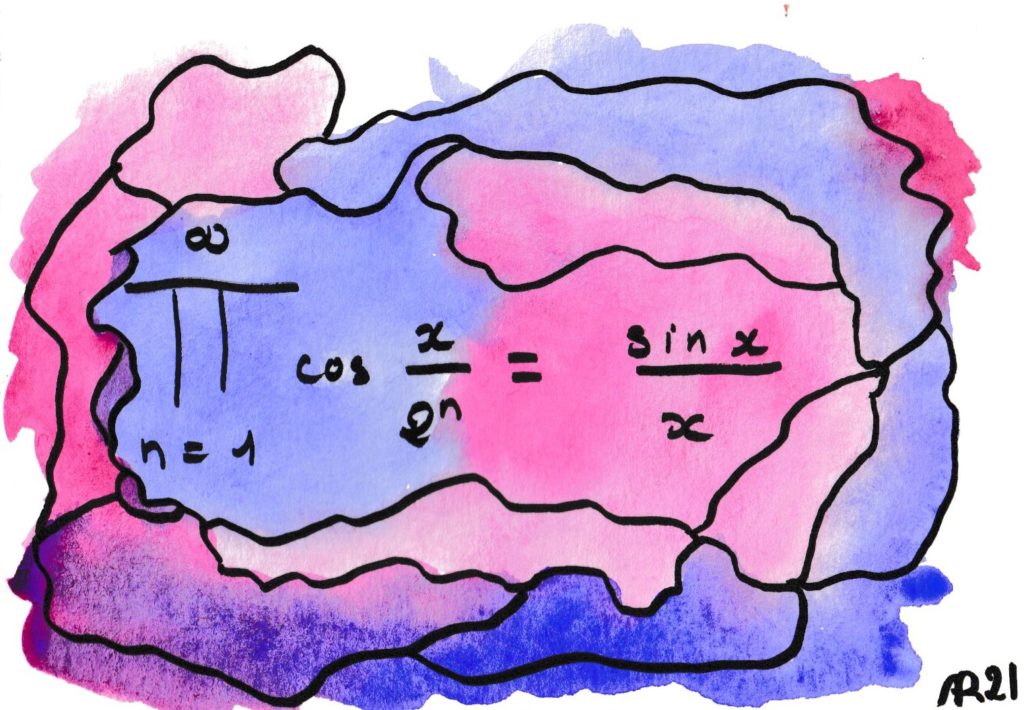
Pour une fois, la formule mathématique se heurte au réel de façon inattendue. Le produit de gauche représente, quand on l’arrête à un nombre fini de termes, un signal parfaitement périodique, mais sa période devient de plus en plus grande. Au point qu’en faisant passer ce signal dans un haut-parleur, la fréquence devient si basse qu’on dépasse la perception de la périodicité. À la limite, on trouve le fameux sinus cardinal qui exhibe un net diminuendo (amortissement du son) qui n’existait lors d’aucune des étapes précédentes !

Le nombre 42 est le plus célèbre de la culture « nerd » à cause du chef d’œuvre de SciFi déjantée de Doug Adams, La vie, l’univers et le reste. Pourquoi 42 ? Pourquoi 6 × 9 ? Lisez la trilogie (en plus elle fait 5 tomes) et vous le saurez !
En attendant, la formule est VRAIE… mais en base 13 ! En effet 4 × 13+2 =54 = 6 × 9 (calcul effectué en base 10…).

Cette addition, parfaitement juste, pourra néanmoins surprendre ceux qui ignorent qu’il y a 10 sortes de gens : ceux qui savent compter en binaire… et les autres.
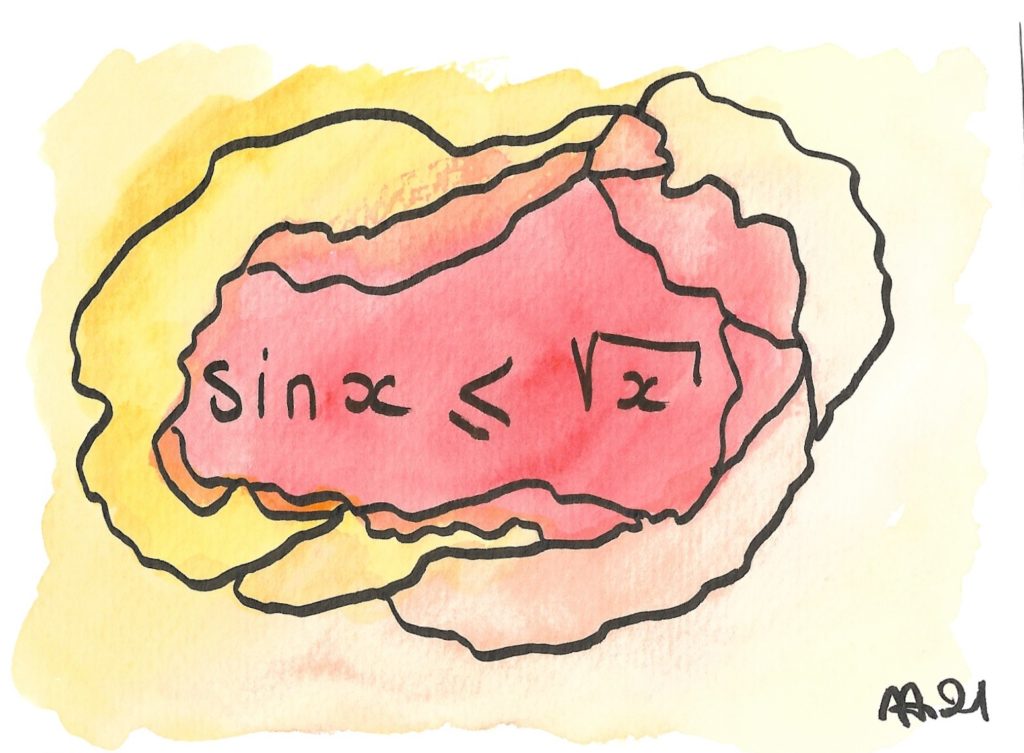
Cette inégalité n’est pas très connue. Elle pourrait bien avoir été découverte par un de mes étudiants, qui a mélangé deux majorations bien connues de sin(x) par 1 ou par x — la première est vraie même pour de grandes valeurs de x, la seconde est plus pertinente quand x est voisin de 0 — grâce à leur « moyenne géométrique ».
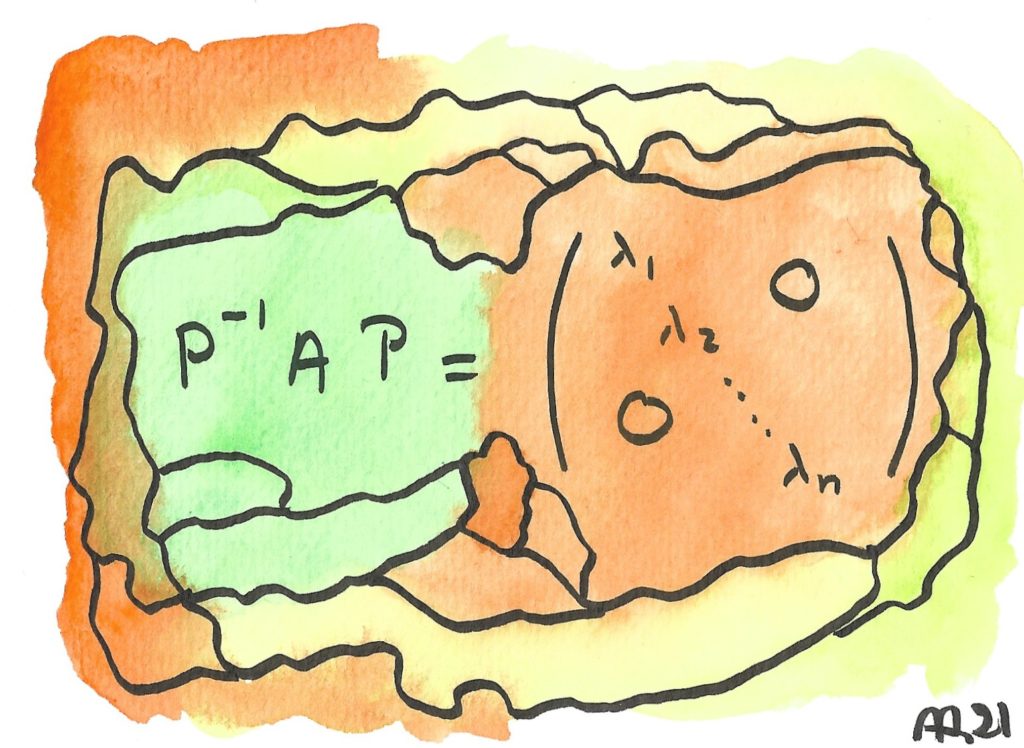
Cette formule exprime la diagonalisation d’une matrice : en changeant de base, c’est à dire de repère dans l’espace, un tableau de nombres enchevêtrés (une matrice) devient miraculeusement simple, avec des 0 partout ailleurs que sur la diagonale ; les équations associées se découplent, c’est à dire que les équations associées peuvent tout d’un coup se résoudre en calcul mental… le tout à condition de réussir cette transformation, qui frise la magie ! Comme le dit Hagrid à Harry Potter pour son 11e anniversaire, « Welcome to Diagonally »
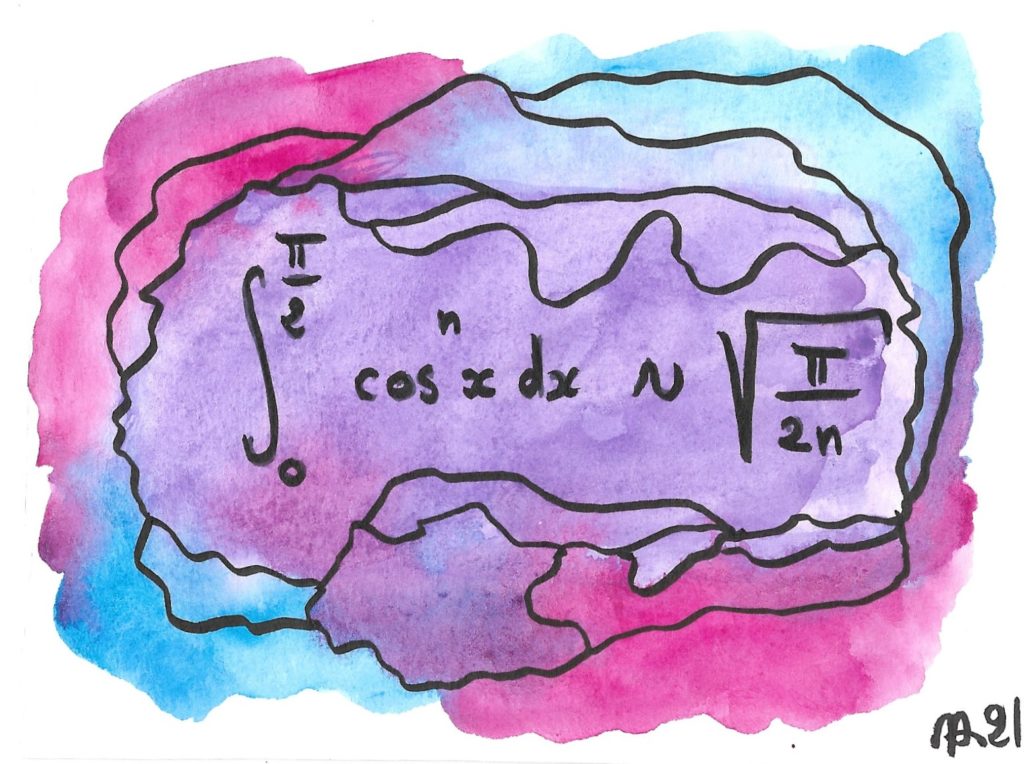
Ces intégrales ont été étudiées par John Wallis, qui décryptait des messages secrets pour la cour d’Angleterre. Il en a tiré la première formule qui donne π comme limite d’une suite de fractions rationnelles. On peut s’étonner, sinon de retrouver le nombre π dans l’équivalent (après tout, il est question de fonctions trigonométriques !) mais sa racine. C’est en fait très général quand on étudie des suites d’intégrales comme celles-ci, dont la valeur se concentre au voisinage d’un point (ici 0, où le cosinus est maximal).
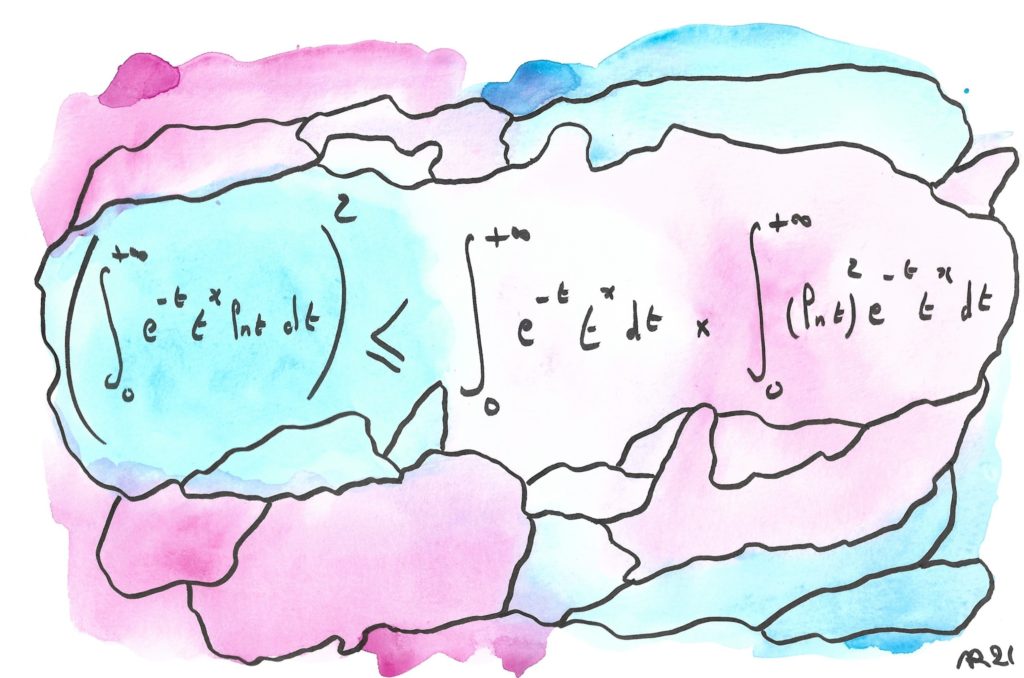
Cette formule traduit la convexité du logarithme de la fonction Gamma, une célèbre « fonction spéciale » qui prolonge la factorielle des nombres entiers (log(Gamma) grimpe de plus en plus vite). On peut la déduire d’une inégalité aussi subtile que célèbre, l’inégalité de Cauchy-Schwarz sous sa forme intégrale :
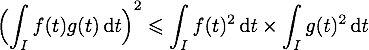
Question : quelles valeurs faut-il prendre pour f et g pour obtenir la formule illustrée ?
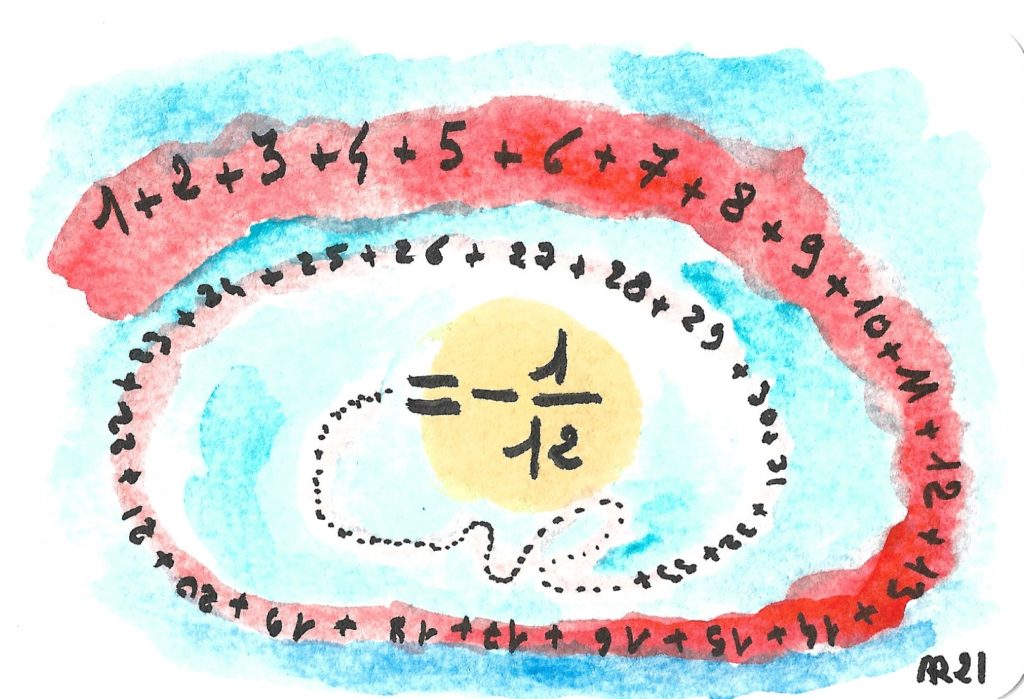
Il est possible d’attribuer des valeurs à certaines séries divergentes comme 1-1+1-1+1-1+1-1… ou 1-2+3-4+5-6+7-8… de façon raisonnable. Mais 1+2+3+4+5+6+7+8+… exagère. Et comment peut-on trouver une valeur négative, alors que tous les termes sont positifs ?
Pourtant on trouve cette valeur en physique des particules, avec une renormalisation (une opération qui consiste à bidouiller un résultat faux jusqu’à ce qu’il devienne vrai) et le même par des manipulations formelles (retrancher ∑ (-1)^n (n+1) pour se ramener à sa valeur). La raison profonde de cette cohérence entre des résultats mal fondés est que cette somme est le prolongement en -1 de la fonction Zeta définie pour s>1 par ∑ 1/n^s. En l’étendant aux nombres complexes, on trouve une formule de symétrie qui relie notamment Zeta(-1) à Zeta(2) [dont la valeur est donnée dans la 4ème formule]. Et on trouve effectivement… -1/12 !
Question : sauriez-vous trouver LA valeur « vraisemblable » de la somme des nombres de Fibonacci, 1+1+2+3+5+8+13+21+… ?
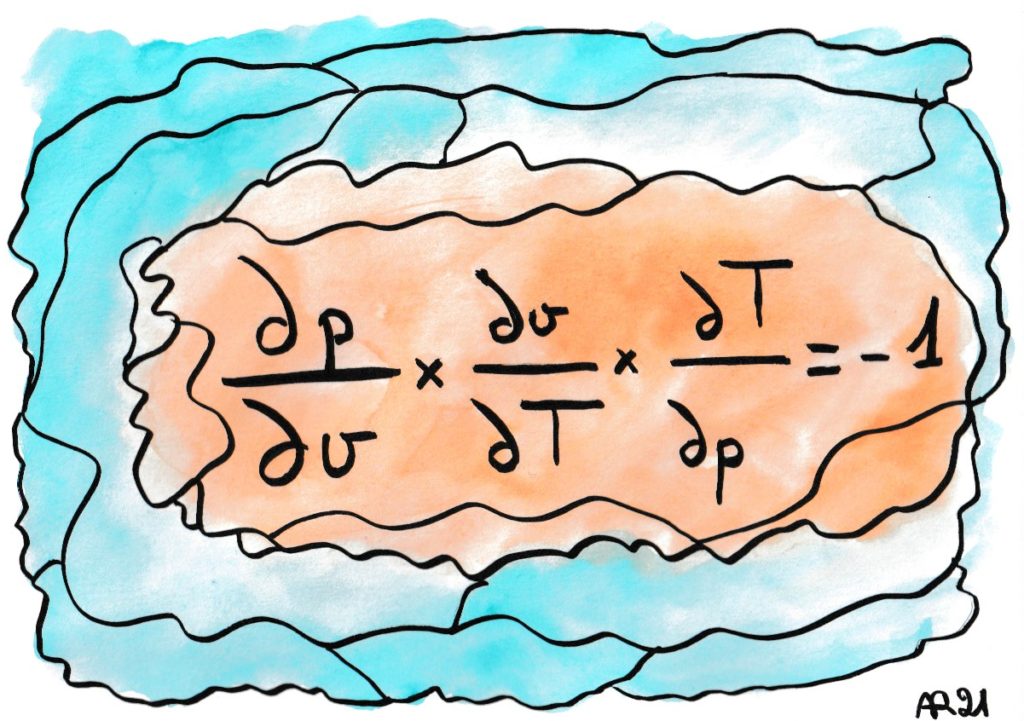
Cette « loi de réciprocité des dérivées partielles » surprend toujours : l’idée derrière ces notations dx/dy est pourtant de faire le rapport entre deux accroissements très petits des quantités x et y, on s’attend donc à trouver un ici un produit égal à +1. Mais la formule cache l’idée physique que les trois variables (p, v, T) sont liées (dans le cas de la thermodynamique d’un gaz parfait, par exemple, on a p×v proportionnel à T).
C’est à dire que dans l’expression d p / d v, v est bien une variable mais p est une fonction de v et de T !

On retrouve tous les chiffres 0 1 2 … 9 dans les décimales de π. Intuitivement c’est évident, ces décimales ayant un côté aléatoire. Mais cela implique-t-il que chacun des chiffres apparaisse avec la même fréquence ? En fait on n’en sait rien ! même si cela est vérifié sur des milliards et des milliards de cas puisque l’on connaît 10^13 décimales. La même question se pose pour toute séquence de chiffres : par exemple, 2021 semble apparaître avec une fréquence de 1/10^4, de même que toute autre séquence de 4 chiffres. Sa première occurrence est au 4351ème chiffre… Vous pouvez chercher votre date de naissance sur la page https://www.angio.net/pi/ !

En essayant de colorier la carte de l’Angleterre, Francis Guthrie a conjecturé en 1852 que 4 couleurs suffisaient pour en faire en sorte que deux régions ayant un bout de frontière commune n’aient jamais la même couleur. Cette conjecture n’est devenue un théorème qu’avec la preuve de Haken en Appel en 1976. Et encore… certains contestent toujours la validité de cette preuve, car elle a eu recours de façon incontournable à l’ordinateur, indispensable pour examiner des milliers de combinaisons différentes. Une preuve qui ne peut pas être vérifiée par un être humain avec papier et crayon est-elle valide ?
La question n’est pas que philosophique : plusieurs erreurs ont été trouvées (et toutes corrigées !) dans le travail des ordinateurs. Néanmoins dans la pratique contemporaine des mathématiciens, le recours à l’ordinateur est devenu très courant et presque universellement accepté. Presque…
Deux remarques : il est relativement facile de prouver que 5 couleurs suffisent pour colorier une carte plane, c’est de descendre à 4 qui a pris plus d’un siècle et imposé l’usage de l’ordinateur. Enfin, sur d’autres surfaces le nombre de couleurs peut être différent : par exemple sur un ruban de Möbius, on peut avoir besoin d’utiliser jusqu’à 6 couleurs !
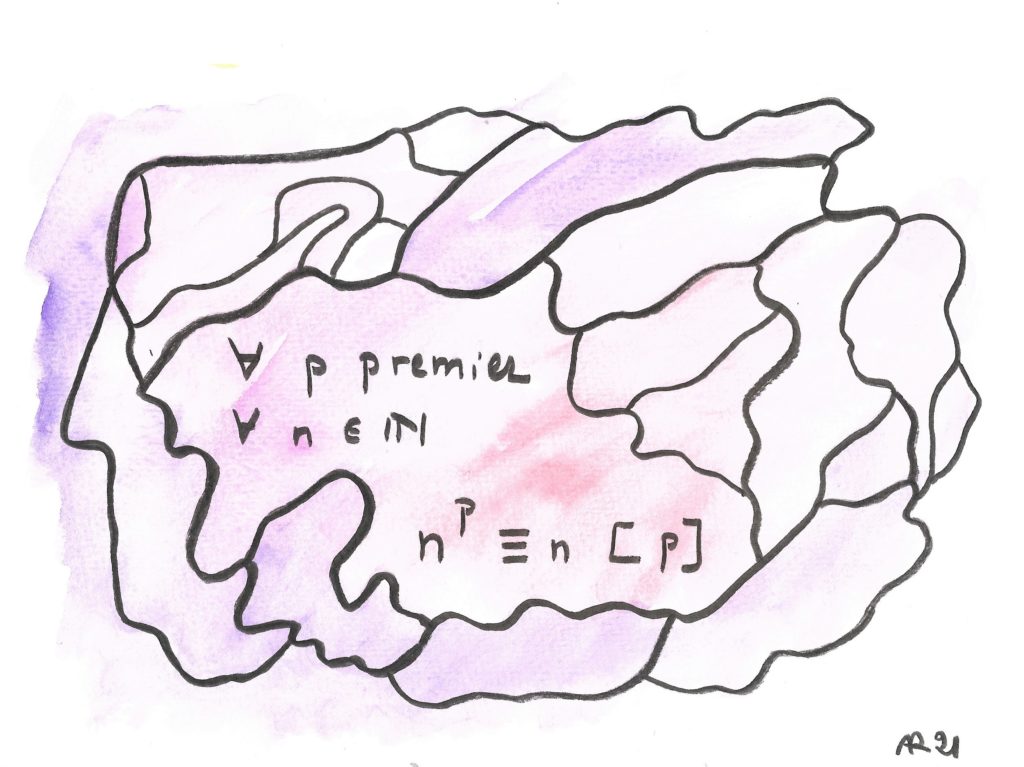
Cet énoncé tout simple semble avoir été découvert par Pierre de Fermat en 1640. Comme les résidus modulo p (en gros les restes de la division par p) ne prennent qu’un nombre fini de valeurs, toute suite de résidus doit forcément repasser par des valeurs égales. Un petit raisonnement montre qua dans ce cas, les puissances de n se mettent alors à tourner en rond, périodiquement. Le théorème affirme que pour toute valeur de n, en p-1 itérations on aura fait (ou plusieurs) tours complets. On peut voir en cela un des tous premiers liens profonds entre l’arithmétique (à la base, l’étude des nombres entiers) et l’algèbre (étude des rapports entre les signes).
Remarque importante : ce théorème marche quand p est premier, mais la réciproque n’est pas vraie. Il existe des nombres pseudo-premiers, comme le fameux nombre de Ramanujan 1729 (cf. —) qui vérifient ce « Petit théorème de Fermat » (sous une forme voisine) sans être premiers tout court.
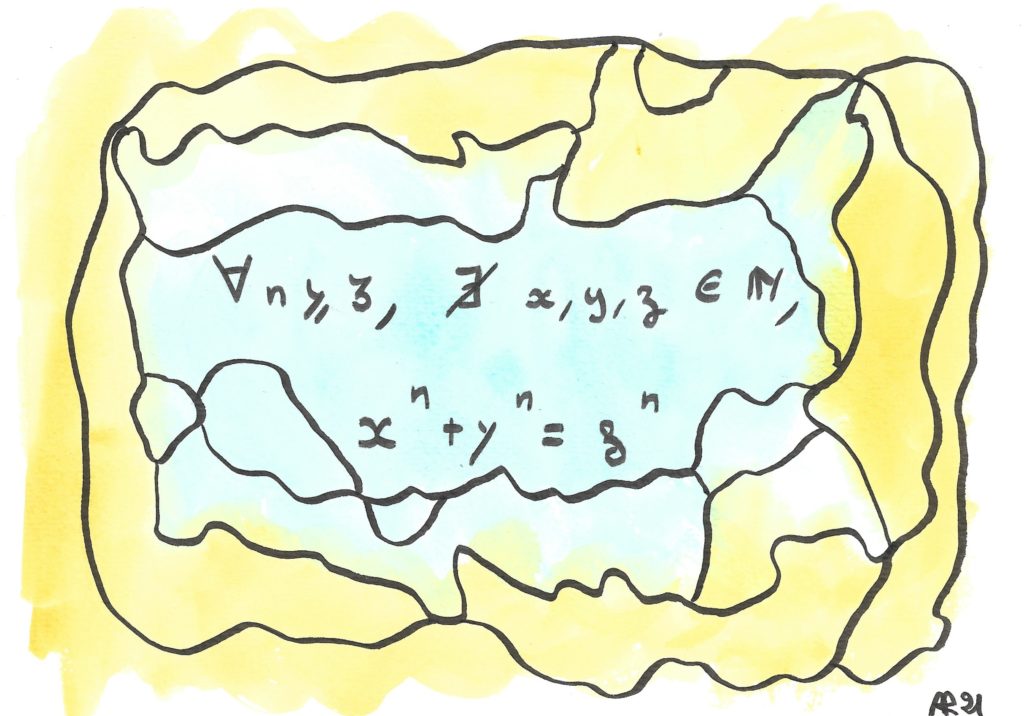
L’impossibilité de cette équation en nombres entiers (sauf si l’un des nombres est nul) a demandé plus de trois siècles avant d’être démontrée.
Pierre de Fermat, magistrat à Toulouse et le plus doué des mathématiciens « amateurs » de toute l’histoire, avait noté dans la marge d’un livre d’exercices que s’il y avait une infinité de solutions pour n=2, il n’y en avait pas pour n=3, n=4, « ni pour les puissances suivantes, et qu’il avait de ce fait une démonstration merveilleuse, que cette marge était trop petite pour contenir ». Ah, ces marges riquiqui ! On le croit sans peine, puisque le corpus des mathématiques élaborées par les innombrables mathématiciens qui ont travaillé sur ce problème pendant plus de trois siècles couvrirait des centaines de milliers de pages. On y trouve le gratin de l’élite : Euler, Sophie Germain, Kummer, tous et toutes auront essayé et parfois avancé.
C’est finalement Andrew Wiles qui parvient en 1994 à démontrer un cas particulier de la conjecture de Taniyama-Weil (sur la paramétrisation de certaines fonctions elliptiques par des fonctions modulaires — et croyez-moi, si vous ne savez pas ce que c’est, vous n’avez pas envie de savoir quel est le rapport !), non sans péripéties, et clôture ainsi plus de trois siècles de recherches qui auront fait progresser les mathématiques plus que tout autre problème.
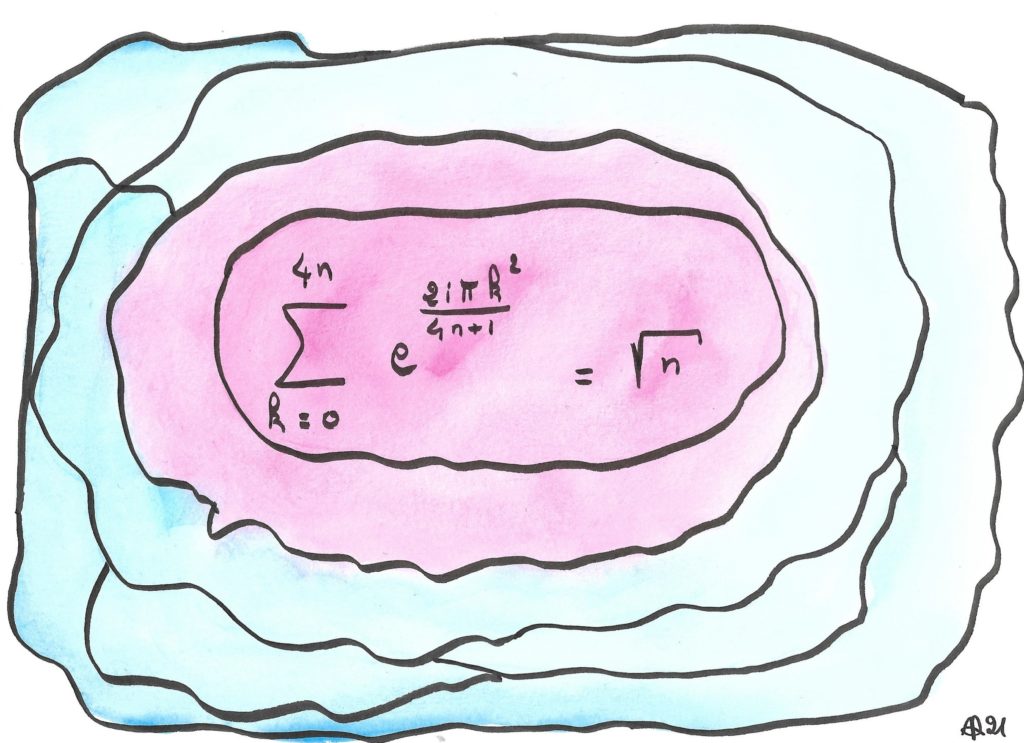
Calculer ce genre de sommes en retirant le « 2 » (qui met l’indice k au carré) est très facile, il s’agit d’un cas particulier de sommes géométriques, additionnant des nombres complexes de module 1, régulièrement disposés sur le cercle unité. C’est l’immense mathématicien Karl Friedrich Gauss qui s’est attaqué à ce cas beaucoup plus complexe (l’écart angulaire augmente entre chaque couple de termes consécutifs), qui est relié à des questions algébriques délicates (invariance sous l’action du groupe des caractères d’un groupe cyclique). De façon amusante, il a trouvé assez vite la valeur de la somme au signe près, mais il lui a fallu plusieurs années supplémentaires pour déterminer ce signe.
Ces « sommes de Gauss » interviennent dans un très beau théorème, la « loi de réciprocité quadratique » qui relie le fait que a soit un carré modulo b à la proposition réciproque.
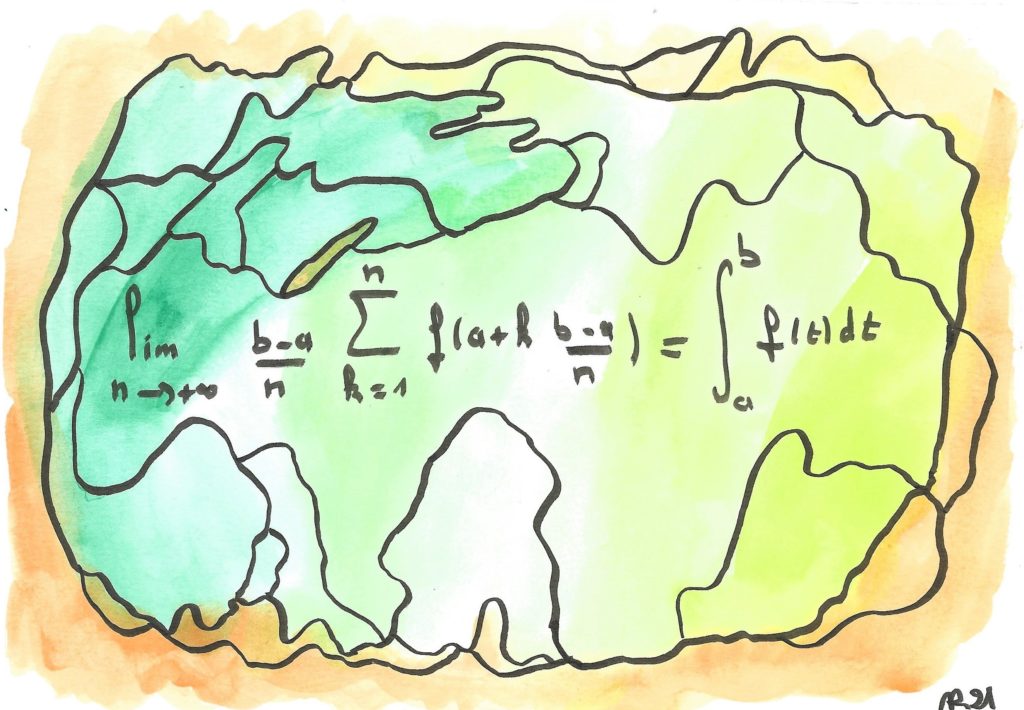
Définition ou théorème ?
L’intégrale vise dès le départ à formaliser et généraliser la notion de « l’aire située sous une courbe » (sous le graphe d’une fonction f). Mais comment peut-on définir cela de façon rigoureuse ?
Il n’y a pas de façon évidente, en tout cas. UN ouvrage de ma bibliothèque recense environ… 200 définitions différentes !
Toutes s’accordent sur l’idée que l’aire d’un rectangle est égale au produit de la base par la hauteur, et que cette notion doit être additive — l’aire de plusieurs rectangles qui se touchent doit être égale à leurs sommes.
Riemann a défini dans sa thèse (en 1865) l’intégrale de f comme la limite, si elle existe, de la somme des aires des rectangles qui s’appuient sur des valeurs régulièrement échantillonnées de la fonction, c’est la formule que vous contemplez : on y a remplacé f par une fonction « constante par morceaux » où les morceaux sont de plus en plus petits. Elle est donc vraie… par définition, pour toute fonction « Riemann-intégrable ». Mais qu’en est-il des autres ?
On peut démontrer que cette définition implique la véracité d’autres définitions, comme celles de Darboux, ou Henstock-Kurzweil. Mais toutes ces notions conservent jalousement certaines fonctions qu’elles peuvent intégrer alors que les autres ne le peuvent pas. Alors c’est quoi, une fonction intégrable ? Peut-être, chère lectrice, cher lecteur, trouverez-vous LA définition qui mettra tout le monde d’accord !
… si elle existe…